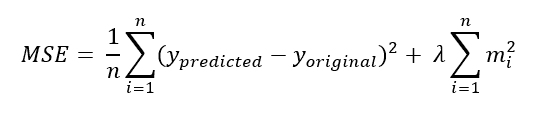Learn L1 and L2 Regularisation in Machine Learning

Summary: L1 and L2 Regularisation in Machine Learning prevent overfitting by adding penalty terms to model parameters. L1 Regularisation selects important features by reducing some coefficients to zero, while L2 Regularisation smooths weight distributions. Choosing the right method ensures optimal model performance, balancing complexity, generalisation, and robustness in predictive analytics.

Introduction

Machine Learning enables computers to learn from data without explicit programming, revolutionising industries with its ability to analyse patterns and make intelligent decisions. 

According to Fortune Business Insights, the global Machine Learning market, valued at $15.44 billion in 2021, is projected to reach $209.91 billion by 2029, growing at a remarkable CAGR of 38.8%. 

However, a key challenge in Machine Learning is overfitting. In overfitting, models memorise data instead of generalising well. Regularisation addresses this issue by adding a penalty to the loss function, improving model performance. 

This blog explores L1 and L2 Regularisation. By reading this blog, you’ll understand the differences between these two techniques and their role in optimising Machine Learning models.

Key Takeaways

• L1 Regularisation (Lasso) eliminates less important features by shrinking some coefficients to zero.
• L2 Regularisation (Ridge) ensures smaller, non-zero weights, improving model generalisation.
• L1 is ideal for feature selection, while L2 is useful when all features are relevant.
• Both methods prevent overfitting, enhancing predictive accuracy.
• Choosing the right regularisation depends on dataset complexity and learning objectives.

What is Regularisation in Machine Learning?

Regularisation is the approach in Machine Learning that prevents overfitting by ensuring that a penalty term is included within the model’s function. There are two main objectives of Regularisation include-

• To reduce the complexity of a model.
• To improve the ability of the model to generalise new inputs.

Numerous Regularisation methods add different penalty terms, including L1 and L2 Regularisation. While L2 Regularisation is a punishment term based on the squares of the given parameters, L1 is a penalty term for absolute values of the model’s parameters. 

Certainly, Regularisation reduces the chances of overfitting and controls the model’s parameters. Therefore, it helps enhance the model’s performance on untested data.

What is L1 Regularisation?

L1 Regularisation, or Lasso Regularisation, is a Machine Learning strategy that inhibits overfitting by introducing a penalty term in the model’s loss function. The penalty term is based on the absolute values of the model’s parameters. 

L1 Regularisation tends to reduce the parameters of some models to zero to lower the number of non-zero parameters in the model.

L1 Regularisation is useful when working with high-dimensional data. It enables you to choose a subset of the most essential attributes. Furthermore, it helps reduce the risk of overfitting and makes the model easier to understand. Hyperparameter lambda regulates the strength of L1 Regularisation by controlling the size of the penalty term. 

Thus, improvement in Regularisation occurs when lambda rises, and the parameters are reduced to zero.

The L1 Regularisation formula is given below: 

What is L2 Regularisation?

L2 Regularisation, also known as Ridge Regularisation, is an approach in Machine Learning. It avoids overfitting by executing penalty terms in the model’s loss functions on the squares of the model’s parameters. The primary goal of L2 Regularisation is to ensure that the model’s parameters have short sizes and prevent oversizing.

For L2 Regularisation, the term proportionate to the squares of the model’s parameters is added to the loss function. It works by limiting the size of the parameters and preventing them from growing out of control. The hyperparameter lambda, which controls the Regularisation’s intensity, also ensures the size of the penalty term is controlled. Hence, the parameters will be smaller, and the Regularisation will be stronger with the greater lambda.

The L2 Regularisation formula is given below: 

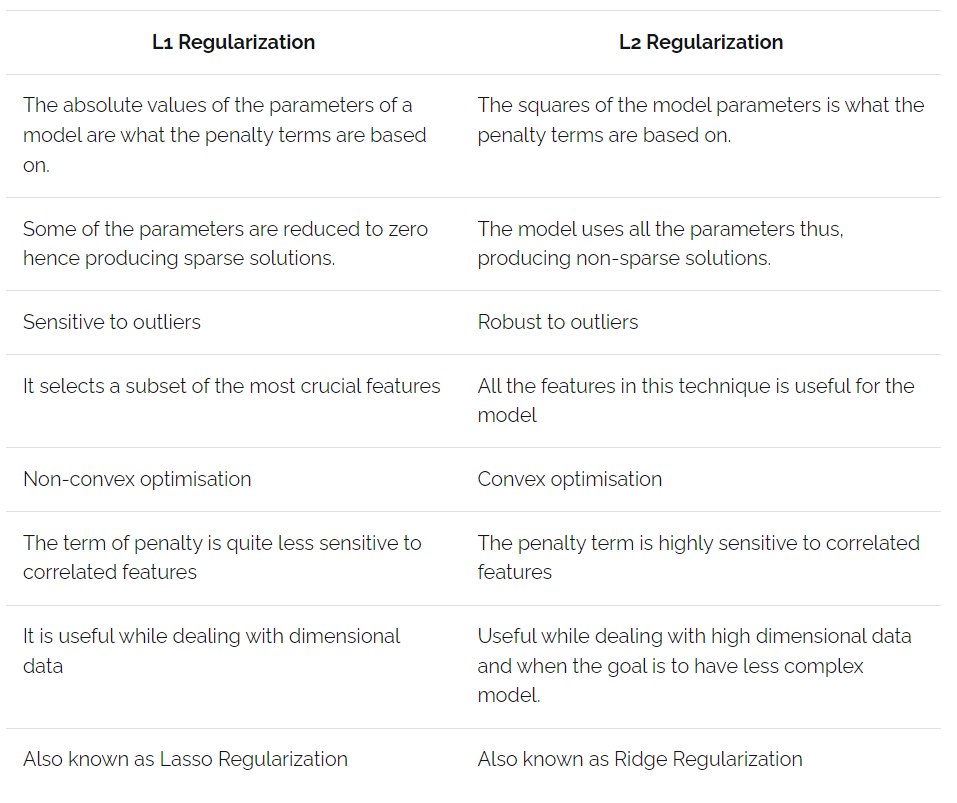
Differences Between L1 and L2 Regularisation

While L1 and L2 Regularisation aims to mitigate overfitting by adding a penalty to the model’s parameters, they do so differently, leading to unique impacts on the model’s performance and structure. Understanding these differences is crucial for selecting the appropriate Regularisation technique based on the specific requirements of your Machine Learning task.

L1 Regularisation

L1 Regularisation, also known as Lasso (Least Absolute Shrinkage and Selection Operator), is characterised by adding the absolute values of the model parameters as a penalty term. This approach has several distinctive features and implications:

• Penalty Term: Based on the absolute values of the model parameters.
• Sparse Solutions: Some parameters are reduced to zero, producing sparse solutions.
• Sensitivity to Outliers: More sensitive to outliers compared to L2 Regularisation.
• Feature Selection: Selects a subset of the most crucial features, effectively performing feature selection.
• Non-convex Optimisation: Typically involves non-convex optimisation, which can be more challenging.
• Insensitive to Correlated Features: The penalty term is less sensitive to correlated features.
• Dimensional Data: Useful when dealing with dimensional data, especially in high-dimensional spaces.
• Also Known As: Commonly referred to as Lasso Regularisation.

L2 Regularisation

L2 Regularisation, also known as Ridge Regularisation, involves adding the squares of the model parameters as a penalty term. This technique offers a different set of advantages and characteristics:

• Penalty Term: Based on the squares of the model parameters.
• Non-sparse Solutions: Uses all the parameters, producing non-sparse solutions.
• Robustness to Outliers: More robust to outliers than L1 Regularisation.
• Feature Utilisation: All features are helpful for the model, contributing to the final predictions.
• Convex Optimisation: Involves convex optimisation, which is easier to solve compared to non-convex optimisation.
• Sensitivity to Correlated Features: The penalty term is highly sensitive to correlated features, affecting model performance.
• High-Dimensional Data: Useful for high-dimensional data and when the goal is to have a less complex model.
• Also Known As: Commonly referred to as Ridge Regularisation.

Tabular Representation of Key Differences between L1 and L2

As you know, understanding the critical differences between L1 and L2 Regularisation helps choose the proper method for specific Machine Learning problems. For your clear understanding, let’s look at a tabular representation of the critical differences between L1 and L2 Regularisation methods.

Practical Applications of L1 and L2 Regularisation

The choice between L1 and L2 Regularisation hinges on the specific characteristics and requirements of the Machine Learning problem. Each method has unique advantages and is suited to different scenarios. Here are some practical considerations to guide the selection process:

The choice between L1 and L2 Regularisation depends on the specific characteristics and requirements of the Machine Learning problem. Here are some practical considerations for each technique:

When to Use L1 Regularisation

L1 Regularisation is ideal for scenarios where feature selection and sparsity are essential. Here are some specific cases where L1 Regularisation excels:

• Feature Selection: L1 Regularisation is highly effective when identifying and retaining essential features. It reduces the number of features by setting some coefficients to zero, effectively performing feature selection.
• Dimensional Data: When dealing with datasets with many features, L1 Regularisation can help manage dimensionality. Producing sparse solutions simplifies the model and makes it easier to interpret.
• Irrelevant or Redundant Features: If you suspect that a subset of the features in your dataset is irrelevant or redundant, L1 Regularisation can help. It tends to shrink the coefficients of less important features to zero, thus removing them from the model and improving performance.

When to Use L2 Regularisation

L2 Regularisation is suitable for scenarios where the use of all features and robustness to outliers are crucial. Here are some specific cases where L2 Regularisation is beneficial:

• All Features Relevant: When you believe all features in your dataset contribute to the outcome, L2 Regularisation is appropriate. Unlike L1, it does not shrink any coefficients to zero, ensuring that all features are included in the model.
• Robustness to Outliers: L2 Regularisation is more robust to outliers than L1. If your dataset contains outliers that could significantly influence the model, L2 Regularisation can help mitigate their impact, leading to more stable and reliable predictions.
• High-Dimensional Data and Less Complex Models: When dealing with high-dimensional data where the goal is to reduce model complexity, L2 Regularisation is useful. It helps to smooth the coefficients, resulting in a simpler and more generalisable model.

After carefully considering your Machine Learning problem’s specific needs, you can choose between L1 and L2 Regularisation to achieve optimal performance and model interpretability.

Conclusion

L1 and L2 Regularisation in Machine Learning prevent overfitting and improve model performance. L1 Regularisation enhances feature selection by shrinking some coefficients to zero, making it ideal for high-dimensional data.

 L2 Regularisation, on the other hand, ensures smoother weight distributions, making models more robust. Choosing the proper regularisation method depends on the specific dataset and learning objective. 

While L1 is best for sparsity and feature selection, L2 helps when all features contribute to predictions. Understanding their differences allows data scientists to build more efficient, generalisable models that perform well on unseen data.

Frequently Asked Questions

What is the Difference Between L1 and L2 Regularisation in Machine Learning?

L1 Regularisation (Lasso) penalises absolute parameter values, leading to sparse solutions and feature selection. L2 Regularisation (Ridge) penalises squared parameter values, ensuring smaller, non-zero weights and reducing overfitting while maintaining all features in the model.

When Should You Use L1 Regularisation in Machine Learning?

Use L1 Regularisation when feature selection is necessary, especially for high-dimensional datasets. It eliminates irrelevant features by setting some coefficients to zero, simplifying the model and improving interpretability. L1 is ideal when dealing with redundant or unnecessary variables.

How Does L2 Regularisation Improve Model Performance?

L2 Regularisation prevents overfitting by adding a squared penalty to large model parameters, ensuring smoother weight distributions. It helps when all features contribute to predictions and improve the model’s generalisation by reducing variance, leading to better performance on unseen data.