Understanding Orthogonality in Linear Algebra: Definition and Fundamentals

Summary: Orthogonality in linear algebra signifies the perpendicularity between vectors, with orthogonal vectors having a zero dot product. Orthonormal vectors are orthogonal and have unit length, simplifying mathematical operations and computations.

Introduction

Linear algebra is a branch of mathematics focused on vector spaces and linear transformations. It is crucial in numerous fields, from computer graphics to Machine Learning. Orthogonality, a key concept in linear algebra, refers to the perpendicularity between vectors. Understanding orthogonal and orthonormal vectors is essential for solving complex problems efficiently. 

This blog aims to clarify the concept of orthogonality, explore its definitions, and highlight its applications. By the end, you’ll grasp the significance of orthogonal and orthonormal vectors and their impact on various practical and theoretical aspects of linear algebra.

Read Blogs: 

Eigen-decomposition Applications: A Comprehensive Guide.

Understanding the Functional Programming Paradigm.

What is Orthogonality?

Orthogonality refers to the concept of perpendicularity in the context of vectors and matrices. Two vectors are orthogonal in vector spaces if their dot product equals zero. This means they are at a right angle to each other in the vector space. 

For instance, in a 2D plane, the vectors v=(1,0) and w=(0,1) are orthogonal because their dot product is 1×0+0×1=0.

When dealing with matrices, orthogonality extends to matrices where columns (or rows) are orthogonal vectors. An orthogonal matrix is a square matrix whose columns and rows are mutually orthogonal unit vectors. Mathematically, if Q is an orthogonal matrix, then 

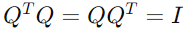
where is the transpose of Q and I is the identity matrix.

Understanding orthogonality is crucial as it simplifies many linear algebra operations, such as solving linear systems and performing decompositions. It also plays a significant role in areas like computer graphics and Data Analysis.

Explore: Mastering Mathematics For Data Science.

Orthogonal and Orthonormal Vectors in Linear Algebra

Orthogonality and orthonormality are foundational concepts in linear algebra that play crucial roles in various mathematical and practical applications. Understanding these concepts helps grasp more complex topics, such as matrix transformations, signal processing, and optimisation problems.

Definition of Orthogonal Vectors

In linear algebra, two vectors are considered orthogonal if their dot product equals zero. Mathematically, for two vectors u and v, they are orthogonal if:

This implies that the vectors are perpendicular to each other in the vector space. Orthogonality extends beyond vectors to include spaces and subspaces, where two subspaces are orthogonal if every vector in one subspace is orthogonal to every vector in the other subspace.

Definition of Orthonormal Vectors

Orthonormal vectors take the concept of orthogonality a step further. A set of vectors is orthonormal if each vector is orthogonal to every other vector in the set and each vector has a magnitude of one. In mathematical terms, a set of vectors {v1,v2,…,vn} is orthonormal if:

Orthonormal vectors form an orthonormal basis for a vector space, simplifying many computations and analyses.

Differences Between Orthogonal and Orthonormal Vectors

The primary difference between orthogonal and orthonormal vectors lies in the normalisation condition. While orthogonal vectors need only be perpendicular, orthonormal vectors must also have a unit length. Orthogonality does not imply normalisation, and vice versa. In essence:

• Orthogonal Vectors: Only require that the dot product between them is zero, indicating they are perpendicular but not necessarily of unit length.
• Orthonormal Vectors: Require orthogonality; each vector has a length of one, ensuring both perpendicularity and unit magnitude.

Examples of Orthogonal and Orthonormal Vectors

Example 1: Orthogonal Vectors

Consider the vectors a=(1,2) and b=(−2,1). To check if these vectors are orthogonal, compute their dot product:

Since the dot product is zero, a\mathbf{a}a and b\mathbf{b}b are orthogonal vectors.

Example 2: Orthonormal Vectors

Consider the vectors . To determine if they are orthonormal:

Since the dot product is not zero, these vectors are not orthogonal. Instead, let’s normalise them:

Both vectors have one magnitude, but they need to be perpendicular to be orthonormal. The correct example of orthonormal vectors could be , which are unit vectors and orthogonal to each other.

Understanding the distinction between orthogonal and orthonormal vectors is essential for various mathematical operations and applications. Orthonormal vectors, in particular, simplify computations and are a cornerstone in many applied mathematics and engineering areas.

Further Explore: 

Skills Required for Data Scientist: Your Ultimate Success Roadmap.

Your Roadmap to Learn AI from Scratch 2024.

Mathematical Definition

Orthogonality is a fundamental concept in linear algebra, crucial for understanding vector spaces and matrix operations. This section delves into the formal definition of orthogonal vectors, explores the properties of orthogonal matrices, and provides examples to illustrate these concepts.

Formal Definition of Orthogonal Vectors

Two vectors are orthogonal if their dot product equals zero. Mathematically, for vectors u and v, they are orthogonal if:

This condition implies that the vectors are perpendicular to each other in the geometric sense. Orthogonality extends to multiple vectors as well. A set of vectors is orthogonal if every pair of distinct vectors is orthogonal.

Orthogonal Matrices and Their Properties

An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors. Formally, a matrix Q is orthogonal if:

where QT denotes the transpose of Q\, and I is the identity matrix. Key properties of orthogonal matrices include:

• The rows and columns of an orthogonal matrix form an orthonormal set.
• Orthogonal matrices preserve vector norms and angles.
• The inverse of an orthogonal matrix is equal to its transpose.

Examples of Orthogonal Vectors and Matrices

Consider vectors a=[1,0] and b=[0,1]. Their dot product is 1⋅0+0⋅1=0, so a and b are orthogonal.

For matrices, the identity matrix I is an example of an orthogonal matrix, as:

Orthogonal matrices are essential in simplifying many linear algebra problems and preserving geometric properties during transformations.

See: Data Science Tools That Will Change the Game in 2024.

Orthogonality in Vector Spaces

Orthogonality in vector spaces is a fundamental concept in linear algebra that revolves around the relationships between vectors. Understanding how vectors interact in multidimensional spaces, particularly regarding their relative angles and projections, is essential. This section delves into key aspects of orthogonality, including the inner product, orthogonal projections, and orthogonal complements and subspaces.

Concept of Inner Product (Dot Product)

The inner product, or the dot product, is a crucial tool for determining orthogonality between vectors. For two vectors u and v in an n-dimensional space, their inner product is calculated as:

If the inner product of u and v equals zero, the vectors are orthogonal. This means they are perpendicular to each other in the vector space, forming a right angle. The inner product provides a measure of orthogonality and helps calculate vector lengths and angles between vectors.

Orthogonal Projections

Orthogonal projection involves projecting one vector onto another so that the projection is orthogonal to the vector’s complement. Given a vector v\mathbf{v}v and a subspace spanned by u, the orthogonal projection of v onto u is given by:

This projection minimises the distance between v, and the subspace spanned by u, making it a key concept in the least squares approximation and data fitting.

Orthogonal Complements and Subspaces

The orthogonal complement of a subspace W within a vector space is the set of all vectors that are orthogonal to every vector in W. Mathematically, if WWW is a subspace of , its orthogonal complement consists of vectors v such that:

Understanding orthogonal complements helps in analysing vector space decompositions and solving systems of linear equations.

More: Mathematics And Data Science: Its Role and Relevance.

Orthogonality in Matrix Theory

Orthogonality in matrix theory is crucial in simplifying complex linear algebra problems. Central to this topic, orthogonal matrices have special properties that make them valuable in various applications.

Definition and Properties of Orthogonal Matrices

An orthogonal matrix is a square matrix whose rows and columns are orthonormal vectors. Formally, a matrix Q is orthogonal if , where QT denotes the transpose of Q and I is the identity matrix. This property implies that the matrix Q preserves vector norms and angles, making it ideal for transformations that do not alter the geometric structure of the data. Orthogonal matrices have several beneficial properties, including their inverse equals their transpose and preserving the dot product between vectors.

Eigenvalues and Eigenvectors of Orthogonal Matrices

The eigenvalues of an orthogonal matrix have notable characteristics. Specifically, they lie on the unit circle in the complex plane. This means that if λ is an eigenvalue of an orthogonal matrix Q, then ∣λ∣=1.

Moreover, the eigenvectors corresponding to different eigenvalues of an orthogonal matrix are orthogonal to each other. This property simplifies many problems in numerical analysis and signal processing.

QR Decomposition and Its Relation to Orthogonality

QR decomposition is a fundamental technique that utilises orthogonality. In QR decomposition, a matrix A is factored into the product of an orthogonal matrix Q and an upper triangular matrix R.

This factorisation simplifies solving linear systems and least squares problems. The orthogonal matrix Q ensures that the transformation preserves the structure of the original matrix, while the upper triangular matrix R facilitates straightforward computational procedures.

Orthogonality in matrix theory provides a robust framework for efficiently analysing and solving various linear algebra problems.

Check: Easy Way To Learn Data Science For Beginners.

Applications of Orthogonality

Orthogonality plays a crucial role in various mathematical and practical applications. Understanding its applications can reveal the power and versatility of this concept in solving complex problems.

Orthogonalisation Processes

One primary application of orthogonality is in orthogonalisation processes, with the Gram-Schmidt process being a prominent example. The Gram-Schmidt process converts a set of linearly independent vectors into an orthonormal basis for the vector space. 

This process simplifies many mathematical operations, such as solving systems of linear equations or performing matrix decompositions. By ensuring that vectors are orthogonal, the Gram-Schmidt process helps avoid redundant calculations and improves numerical stability.

Use in Least Squares Approximation and Data Fitting

Orthogonality is fundamental in least squares approximation, a technique for finding the best-fitting solution to an overdetermined system of equations. In least squares problems, orthogonal projection helps minimise the error between the observed data and the model. 

By projecting data onto an orthogonal basis, the solution becomes computationally efficient and more accurate, particularly useful in regression analysis and curve fitting.

Importance in Signal Processing and Numerical Methods

In signal processing, orthogonality ensures that signals are represented in a way that minimises interference and maximises clarity. Orthogonal functions or basis sets, such as those used in Fourier transforms, enable efficient signal representation and processing. This orthogonality aids in separating and analysing different frequency components of a signal.

In numerical methods, orthogonality simplifies calculations and improves algorithm performance. For instance, orthogonal matrices are used in QR decomposition, essential for solving linear systems and performing eigenvalue computations. Using orthogonal transformations can also enhance the accuracy and stability of numerical simulations.

Overall, orthogonality is a versatile tool in theoretical and applied mathematics, providing robust solutions across various fields.

Look At: How to become a Statistician without a Degree?

Fundamental Theorems and Results

Understanding the fundamental theorems related to orthogonality provides crucial insights into linear algebra and vector space theory. These theorems highlight the significance of orthogonal relationships between vectors and their impact on mathematical operations and proofs.

Pythagorean Theorem in the Context of Orthogonality

The Pythagorean theorem, a cornerstone of geometry, extends naturally into linear algebra when considering orthogonal vectors. 

In Euclidean space, if two vectors are orthogonal, the square of the length of their resultant vector equals the sum of the squares of their lengths. Mathematically, if u and v are orthogonal vectors, then:

This relationship mirrors the classic Pythagorean theorem in the context of vector spaces. This property is vital for computations involving orthogonal projections and least squares approximations, ensuring that the errors in these calculations are minimised and well understood.

The Role of Orthogonality in Vector Space Theory

Orthogonality plays a pivotal role in vector space theory by facilitating the decomposition and simplification of complex problems. In any vector space with an inner product, orthogonal vectors form a basis for simplifying computations. For example, in orthogonal vector spaces, projections onto subspaces become straightforward, and computations involving linear transformations become more manageable.

Orthogonal bases, such as those found in the Gram-Schmidt process, decompose vector spaces into mutually perpendicular components. This decomposition helps solve systems of linear equations, optimise algorithms, and perform various applications in Data Analysis and signal processing. 

By leveraging orthogonality, mathematicians and engineers can achieve more apparent, more efficient solutions to complex problems, emphasising its foundational importance in linear algebra.

Common Misconceptions

Orthogonality is a fundamental concept in linear algebra, yet several misconceptions often arise. Clarifying these misunderstandings can enhance your grasp of the topic and prevent confusion.

Orthogonality Means Perpendicularity Only in 2D or 3D

Many believe that orthogonality only applies to two-dimensional or three-dimensional spaces. In reality, orthogonality extends to higher dimensions as well. Vectors can be orthogonal in any dimensional space, not just the familiar 2D or 3D contexts.

Orthogonal Vectors Are Always Unit Vectors

Some assume that orthogonal vectors must also be unit vectors (having a magnitude of 1). However, orthogonality only requires that the dot product of the vectors is zero. The vectors can have any magnitude; orthonormal vectors, which are both orthogonal and unit vectors, are a specific case.

Orthogonality Implies Independence

While orthogonal vectors are linearly independent, the converse isn’t always true. Vectors can be independent without being orthogonal. Orthogonality is a stronger condition that implies independence, but not every set of independent vectors is orthogonal.

Understanding these misconceptions helps in applying orthogonality correctly across various linear algebra problems.

Closing Statements

Orthogonality is a fundamental concept in linear algebra, emphasising the perpendicularity of vectors. Understanding orthogonal and orthonormal vectors is crucial for simplifying complex problems and performing efficient computations. This knowledge is essential in various fields, including Data Analysis and signal processing, where orthogonality aids in accurate and stable solutions.

Frequently Asked Questions

What is Orthogonality in Linear Algebra? 

Orthogonality in linear algebra refers to the perpendicularity between vectors. Two vectors are orthogonal if their dot product equals zero, indicating they are at right angles to each other in the vector space.

How do Orthogonal Vectors Differ From Orthonormal Vectors? 

Orthogonal vectors are perpendicular with a dot product of zero, while orthonormal vectors are orthogonal and have a unit length. Orthonormal vectors form an orthonormal basis for vector spaces, simplifying computations.

What are the Applications of Orthogonality in Linear Algebra? 

Orthogonality simplifies linear algebra problems, aiding in matrix decompositions, least squares approximations, signal processing, and numerical methods. It ensures accurate solutions and enhances computational efficiency.