Summary: LASSO Regression performs variable selection and regularisation by shrinking some coefficients to zero. This simplifies models, enhances interpretability, and prevents overfitting, especially in high-dimensional data. It’s ideal for identifying significant predictors while maintaining model accuracy and robustness.
Introduction
LASSO Regression, short for Least Absolute Shrinkage and Selection Operator, is a powerful statistical method that enhances linear regression by performing variable selection and regularisation. This technique is precious in high-dimensional data settings where numerous predictors may complicate model building.
By shrinking some coefficients to zero, LASSO effectively identifies and retains only the most significant variables, simplifying the model and improving interpretability.
This comprehensive guide will delve into the mechanics of LASSO Regression, its advantages, practical applications, and implementation strategies, providing you with the knowledge to leverage this method for robust, efficient predictive modelling.
Basics of Regression Analysis
Regression analysis is a statistical technique for examining the relationship between a dependent variable and one or more independent variables. The simplest form is linear regression, in which the relationship is modelled using a straight line.
The equation of this line is:
Y = β0 + β1X + ϵ.
where Y is the dependent variable, X is the independent variable, β0 is the intercept, β1 is the slope, and ϵ is the error term.
The primary goal of regression analysis is to predict the dependent variable’s value based on the independent variables’ values and understand their relationships’ strength and nature. It involves estimating the coefficients (β values) that minimise the difference between observed and predicted values.
Beyond linear regression, other types like multiple, polynomial, and logistic regression address more complex relationships. Regression analysis is widely used in various fields such as economics, biology, engineering, and social sciences, to inform decisions and understand trends.
LASSO Regression Overview
LASSO Regression, or Least Absolute Shrinkage and Selection Operator, is a linear regression type incorporating a regularisation technique to enhance model performance and interpretability. Unlike traditional linear regression, LASSO adds a penalty equal to the absolute value of the coefficients’ magnitudes, effectively shrinking some coefficients to zero.
This results in a sparse model where only the most significant predictors are retained, aiding in feature selection.
The critical advantage of LASSO is its ability to handle high-dimensional data where the number of predictors may exceed the number of observations, often seen in fields like genetics, finance, and marketing. LASSO improves prediction accuracy and model simplicity by preventing overfitting and reducing model complexity.
This method benefits datasets with many potentially irrelevant variables, ensuring that only the most impactful ones are included in the final model.
Mathematical Formulation
The mathematical formulation of LASSO Regression involves minimising the sum of squared residuals with an added penalty for the absolute value of the coefficients. The objective function is:
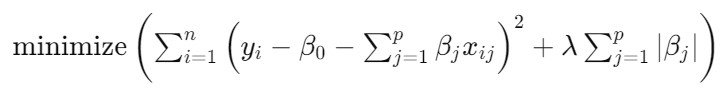
Here, yi are the observed values, xij are the predictors, βj are the coefficients, β0 is the intercept, and λ is the regularisation parameter. The term λ∑j=1p|βj∣ penalises the model complexity, shrinking some coefficients to zero and performing variable selection.
Advantages of LASSO Regression
LASSO regression offers several advantages, particularly for datasets with many features. It performs automatic feature selection by shrinking coefficients towards zero, potentially eliminating irrelevant ones. This leads to simpler, more interpretable models and helps prevent overfitting.
Besides, it offers key advantages, making it a popular choice in Statistical Modeling and Machine Learning. These are listed below:
Feature Selection
LASSO automatically selects important features by shrinking some coefficients to zero, eliminating irrelevant variables from the model. This results in simpler, more interpretable models.
Prevention of overfitting
The regularisation aspect of LASSO helps prevent overfitting by constraining the size of the coefficients. This leads to models that generalise new, unseen data better.
Handling Multicollinearity
LASSO can manage multicollinearity by selecting one variable from a group of highly correlated variables, reducing redundancy and improving model stability.
High-dimensional Data
LASSO is particularly useful in high-dimensional settings where the number of predictors exceeds the number of observations, such as in genomics and finance.
Improved Prediction Accuracy
LASSO often enhances prediction accuracy compared to traditional regression models by focusing on the most relevant variables and reducing noise.
Applications of LASSO Regression
LASSO regression goes beyond just prediction. Its strength lies in identifying the most influential factors. This makes it valuable in various fields, from finance (selecting key drivers of stock prices) to biology (finding genes crucial for a disease). Some notable applications include:
Genomics and Bioinformatics
Gene Selection: In studies aiming to understand genetic contributions to diseases, LASSO helps pinpoint the most significant genes from thousands of potential candidates. This is particularly useful in genome-wide association studies (GWAS).
Personalised Medicine: By identifying specific genetic markers that influence an individual’s response to drugs, LASSO aids in developing personalised treatment plans that improve efficacy and reduce side effects.
Finance
Risk Management: Financial institutions use LASSO to select key predictors of credit risk, such as economic indicators and borrower characteristics, enhancing the accuracy of risk assessment models.
Portfolio Optimization: LASSO can streamline the selection of assets in a portfolio, focusing on those with the most significant impact on returns while controlling for risk, thus aiding in constructing more robust investment strategies.
Marketing
Customer Segmentation: LASSO helps identify the most relevant demographic and behavioural factors that differentiate customer segments, leading to more targeted and effective marketing strategies.
Campaign Optimization: By selecting the key variables that influence marketing campaign success, LASSO enables marketers to fine-tune their approaches, optimise budgets, and improve ROI.
Economics
Economic Growth Models: Economists use LASSO to identify critical factors driving economic growth from various possible predictors, such as investment rates, technological advancements, and labour market conditions.
Policy Impact Analysis: LASSO assists in evaluating the impact of various policy measures by isolating the most influential variables, thereby aiding policymakers in designing more effective economic policies.
Health Care
Predictive Analytics: Healthcare providers use LASSO to predict patient outcomes, such as the likelihood of readmission or disease progression, by selecting the most pertinent clinical variables from electronic health records.
Resource Allocation: By identifying key factors that drive demand for medical services, LASSO helps optimise the allocation of resources, such as staff and equipment, to improve patient care and operational efficiency.
Environmental Science
Air Quality Prediction: LASSO models air quality by selecting the most significant pollutants and environmental factors, enabling more accurate forecasting and better air pollution management.
Climate Change Studies: Researchers use LASSO to identify the most impactful variables affecting climate change from extensive datasets, such as greenhouse gas emissions, deforestation rates, and ocean temperatures, thereby enhancing climate models and informing policy decisions.
Implementing LASSO Regression
Implementing LASSO Regression can significantly enhance your analytical capabilities, particularly when dealing with high-dimensional data like those often encountered in digital marketing and relationship advice analytics. Here’s a step-by-step guide to implementing LASSO Regression in Python using Scikit-learn:
Step-by-Step Implementation
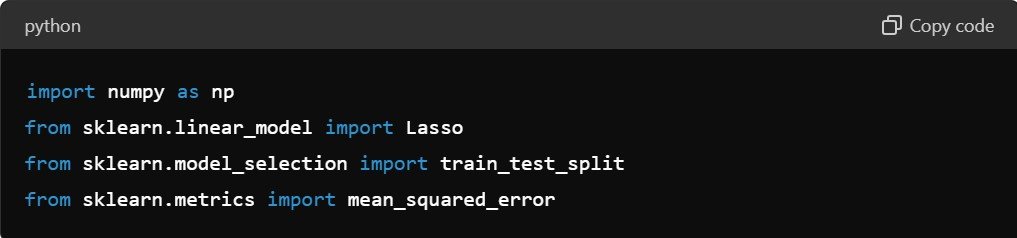
Import Necessary Libraries
Start by importing the necessary libraries. Scikit-learn provides a straightforward implementation of LASSO Regression.
Generate or Load Data
Prepare your dataset. For demonstration purposes, we’ll generate a synthetic dataset. In your case, you might use data from your website’s analytics or other relevant sources.

Split Data into Training and Test Sets
Split the data to evaluate the model’s performance.

Fit the LASSO Model
Initialise the LASSO model with a chosen regularisation strength and fit it to the training data.

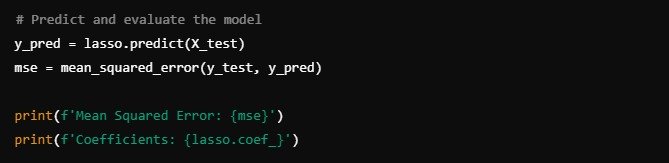
Make Predictions and Evaluate the Model
Use the trained model to make predictions on the test set and evaluate its performance.
Implementing LASSO Regression in these ways can provide valuable insights, helping you optimise your strategies and achieve better results in your various initiatives.
Performance Metrics and Evaluation
Performance metrics and evaluation are crucial for assessing the effectiveness of a LASSO Regression model. The primary metric used is Mean Squared Error (MSE), which measures the average squared difference between the actual and predicted values. Lower MSE indicates better model performance.
Another important metric is the R-squared (R²) value, which indicates the proportion of variance in the dependent variable explained by the independent variables. An R² value closer to 1 signifies a better fit.
Cross-validation techniques, like k-fold cross-validation, ensure the model’s robustness and generalizability. Cross-validation provides a more accurate estimate of model performance by partitioning the data into training and validation sets multiple times.
Additionally, examining the non-zero coefficients in the LASSO model helps understand which predictors are most significant, aiding in feature selection and model interpretability. These metrics and evaluation techniques ensure that the LASSO Regression model is accurate and reliable.
Challenges and Limitations
LASSO regression offers a powerful tool for model simplification, but it has drawbacks. This section highlights these challenges, including selecting the right tuning parameter and handling correlated features.
Bias Introduction
The regularisation term in LASSO introduces bias into the coefficient estimates. While this helps reduce variance and prevent overfitting, it can sometimes lead to underestimating the accurate coefficients, especially for large datasets.
Variable Selection
Although LASSO performs automatic variable selection, it may not always select the best predictors, mainly when dealing with highly correlated variables. In such cases, it might arbitrarily choose one variable from a group of correlated predictors, potentially ignoring other important ones.
Computational Cost
Finding the optimal value for the regularisation parameter (λ\lambdaλ) requires extensive cross-validation, which can be computationally intensive, especially with large datasets or numerous features.
Handling Multicollinearity
While LASSO can manage multicollinearity to some extent, it may not perform as well as other regularisation techniques, such as Ridge Regression, when dealing with highly correlated predictors.
Model Interpretability
Although LASSO simplifies models by shrinking some coefficients to zero, interpreting the remaining non-zero coefficients can still be challenging, mainly when the model includes interactions or polynomial terms.
Data Standardization
LASSO requires all predictors to be on the same scale. Therefore, data standardisation is a necessary preprocessing step, which can be an additional task for practitioners.
Extensions and Variations of LASSO
LASSO Regression has inspired several extensions and variations to address its limitations and enhance its functionality. Notable among these are:
Elastic Net
Combines LASSO’s ℓ1 penalty with Ridge Regression’s ℓ2 penalty, mitigating issues related to multicollinearity and variable selection, especially with highly correlated predictors. It provides a balanced approach, benefiting from both LASSO and Ridge.
Group LASSO
It is useful when predictors are naturally grouped, such as polynomial terms or categorical variables. It enforces sparsity at the group level, selecting or discarding entire groups of variables, making it ideal for fields like genomics.
Adaptive LASSO
This method assigns different weights to penalty terms for different coefficients, improving variable selection consistency and reducing bias. It involves a two-step process using initial estimates to calculate adaptive weights.
Fused LASSO
Designed for temporal or spatial data, it penalises both the magnitude of coefficients and their differences, encouraging smoothness in the coefficient estimates. Thus, it is suitable for time series or spatial datasets.
Sparse Group LASSO
Integrates LASSO and Group LASSO features, promoting within-group sparsity and group-level selection. It is beneficial when expecting a few relevant predictors within some groups.
Bayesian LASSO
It incorporates LASSO into a Bayesian framework, providing a probabilistic interpretation and allowing for prior information incorporation. This offers a way to quantify uncertainty and handle complex modeling scenarios.
These extensions enhance LASSO’s versatility, making it a powerful tool for various complex modelling tasks across diverse fields.
Future Directions and Innovations
Future directions and innovations in LASSO Regression and other shrinkage methods in Machine Learning focus on enhancing model accuracy, interpretability, and computational efficiency. Researchers are exploring hybrid models that combine LASSO with deep learning techniques, improving performance on large, complex datasets.
Additionally, advancements in adaptive algorithms and automated hyperparameter tuning aim to simplify model selection and optimisation. There’s also a growing interest in developing robust versions of LASSO that can more effectively handle outliers and non-linear relationships. These innovations will further solidify the role of shrinkage methods in machine learning, particularly in high-dimensional Data Analysis.
Frequently Asked Questions
What is The Main Advantage of Using LASSO Regression Over Traditional Linear Regression?
The primary advantage of LASSO Regression is its ability to perform both variable selection and regularisation. By adding a penalty for the absolute value of the coefficients, LASSO shrinks some coefficients to zero, effectively eliminating irrelevant predictors.
This results in simpler, more interpretable models and helps prevent overfitting, especially in high-dimensional datasets where the number of predictors is large.
How do I Choose the Regularization Parameter λ in LASSO Regression?
The regularisation parameter λ in LASSO Regression controls the strength of the penalty applied to the coefficients. Choosing the right λ is crucial for balancing model simplicity and accuracy.
Typically, λ is selected through cross-validation, where the dataset is divided into training and validation sets multiple times to evaluate the model’s performance across different values of λ. The value that minimises the cross-validated prediction error is usually chosen.
Can LASSO Regression Handle Multicollinearity AmongPpredictors?
Yes, LASSO Regression can handle multicollinearity to some extent. LASSO effectively reduces the impact of multicollinear predictors by shrinking some coefficients to zero. However, it may arbitrarily select one predictor from a group of highly correlated variables while shrinking the others to zero, which might not always accurately capture the underlying relationships.
In cases of severe multicollinearity, Elastic Net, which combines LASSO and Ridge Regression penalties, maybe a better alternative.
Summing it up
LASSO Regression is a powerful tool for modern Data Analysis, offering significant advantages in feature selection and regularisation. Its ability to handle high-dimensional data and multicollinearity makes it indispensable across various fields.
While challenges such as bias introduction and computational cost exist, extensions like Elastic Net, Group LASSO, and Adaptive LASSO provide effective solutions.
Future innovations promise even more significant enhancements, such as integrating LASSO with advanced Machine Learning techniques and real-time Data Analysis. As these developments unfold, LASSO will continue to be a critical method for building efficient, interpretable, and accurate predictive models.




