Gaussian Mixture Model: A Comprehensive Guide

Summary: The Gaussian Mixture Model (GMM) is a flexible probabilistic model that represents data as a mixture of multiple Gaussian distributions. It excels in soft clustering, handling overlapping clusters, and modelling diverse cluster shapes. Widely used in image segmentation, speech recognition, and anomaly detection, GMM is essential for complex Data Analysis.

Introduction

The Gaussian Mixture Model (GMM) stands as one of the most powerful and flexible tools in the field of unsupervised Machine Learning and statistics. Its ability to model complex, multimodal data distributions makes it invaluable for clustering, density estimation, and pattern recognition tasks.

In this blog, we will explore the core concepts, mathematical foundations, practical applications, and nuances of the Gaussian Mixture Model, ensuring you understand both its elegance and utility.

Key Takeaways

• GMM uses multiple Gaussian components to model complex data distributions effectively.
• Soft clustering assigns probabilities, reflecting uncertainty in cluster membership.
• EM algorithm iteratively optimizes GMM parameters for best data fit.
• GMM handles overlapping and non-spherical clusters better than K-Means.
• Widely applied in image processing, speech recognition, anomaly detection, and finance.

What is a Gaussian Mixture Model?

A Gaussian Mixture Model is a probabilistic model that assumes all the data points are generated from a mixture of several Gaussian distributions with unknown parameters. 

Each Gaussian component represents a cluster or subpopulation within the overall data, and the model assigns probabilities to each data point for belonging to each cluster. Its core components include:

Mixture of Gaussians

GMM models the data as a combination of multiple Gaussian distributions, each characterized by its own mean (μ), covariance (Σ), and mixing coefficient (π).

Soft Clustering

Unlike hard clustering algorithms (e.g., K-Means), which assign each data point to a single cluster, GMM provides a probability (soft assignment) for each point belonging to each cluster.

Parameters:

• Mean (μ): The canter of each Gaussian component.
• Covariance (Σ): The spread or shape of each cluster.
• Mixing Probability (π): The weight or proportion of each Gaussian in the mixture.

Mathematical Foundation

The Gaussian Distribution

A single Gaussian (normal) distribution in DD dimensions is given by:

Mixture Model

The Gaussian Mixture Model with KK components is represented as:

Where:

• πkπk is the mixing coefficient for component kk, with ∑k=1Kπk=1∑k=1Kπk=1 and 0≤πk≤10≤πk≤1

A Gaussian Mixture Model (GMM) works by modelling data as a combination of multiple Gaussian distributions, each representing a cluster. It uses a probabilistic framework to assign data points to clusters based on likelihood, allowing for soft clustering where points can belong to multiple clusters with varying probabilities. Here’s a breakdown of how it operates:

1. Initialization

• Start with initial guesses for the parameters of each Gaussian component:
  • Means (μ): Cluster centres (often initialized randomly or via K-Means).
  • Covariance matrices (Σ): Shape/spread of each cluster.
  • Mixing coefficients (π): Weight of each Gaussian in the mixture.

2. Expectation-Maximization (EM) Algorithm

The EM algorithm iteratively refines the parameters to maximize the likelihood of the data:

E-Step (Expectation)

• Calculate the responsibility of each Gaussian component for every data point. This is the probability that a point xixi belongs to cluster kk:

• Here, γikγik represents how “responsible” component kk is for xixi.

M-Step (Maximization)

• Update the parameters using the responsibilities calculated in the E-step:
  • New mixing coefficients:

πknew=∑i=1NγikNπknew=N∑i=1Nγik

• New means:

New covariance matrices:

• These updates ensure the Gaussians better fit the data weighted by their responsibilities.

3. Convergence

• Repeat E- and M-steps until:
  • The change in log-likelihood between iterations falls below a threshold (epsilon).
  • A maximum number of iterations is reached

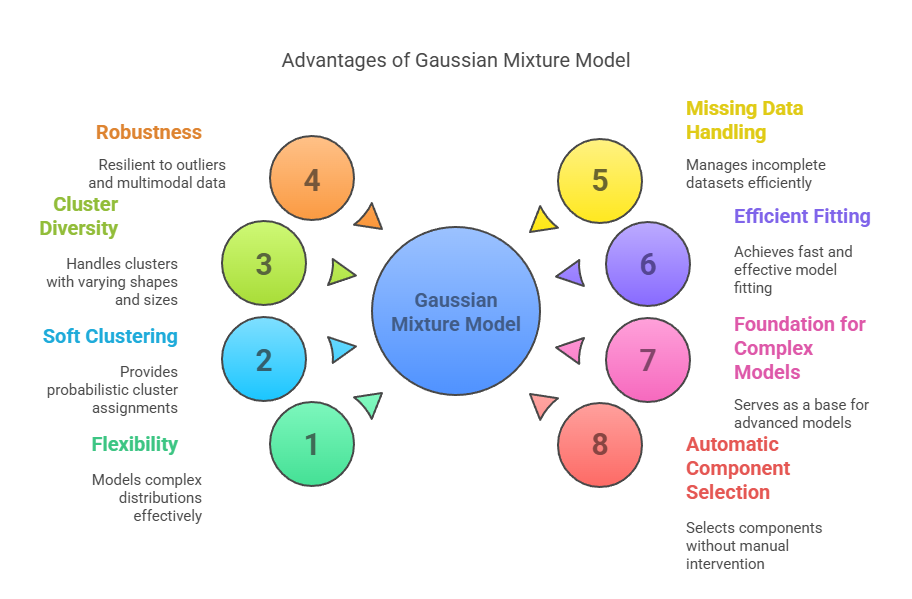
Advantages of Gaussian Mixture Model

The Gaussian Mixture Model (GMM) offers several notable advantages that make it a preferred choice for clustering and density estimation in Machine Learning and Data Analysis:

Flexibility in Modelling Complex Distributions

GMMs can approximate any continuous probability distribution by representing it as a weighted sum of multiple Gaussian components. This flexibility allows them to capture complex, multimodal data patterns that simpler models like K-Means cannot handle effectively.

Soft Clustering with Probabilistic Assignments

Unlike hard clustering algorithms that assign each data point to a single cluster, GMM provides probabilities indicating the likelihood that a point belongs to each cluster. This soft assignment is particularly useful when clusters overlap or data points lie near cluster boundaries.

Ability to Model Clusters with Different Shapes and Sizes

GMMs incorporate covariance matrices for each Gaussian component, enabling them to model elliptical and differently shaped clusters. This contrasts with algorithms like K-Means that assume spherical clusters of equal size.

Robustness to Outliers and Multimodal Data

Because GMMs model data as a mixture of distributions, they can accommodate multiple modes (“peaks”) in the data and are relatively robust to outliers, which might otherwise skew clustering results.

Handling Missing Data

GMMs can marginalize over missing variables, allowing them to handle incomplete datasets more gracefully than some other clustering methods.

Fast and Efficient Fitting

When implemented with the Expectation-Maximization (EM) algorithm, GMMs can be fitted to data relatively quickly, especially with optimized implementations.

Foundation for More Complex Models

GMMs serve as building blocks for advanced probabilistic models such as Hidden Markov Models (HMMs) and Kalman filters, extending their utility beyond clustering.

Automatic Component Selection (with Variational Bayesian GMM)

Some advanced versions of GMM, like the Variational Bayesian Gaussian Mixture Model, can automatically infer the effective number of clusters by shrinking weights of unnecessary components, reducing the need to pre-specify the number of clusters

Applications of Gaussian Mixture Models

Gaussian Mixture Models (GMMs) are widely used across diverse fields due to their flexibility in modeling complex, multimodal data distributions. Below are the primary application areas where GMMs excel:

Clustering and Pattern Recognition

GMMs are extensively used for clustering tasks, especially when clusters have different shapes, sizes, or overlap. They provide soft (probabilistic) assignments, making them ideal for customer segmentation, market research, and data exploration where group boundaries are not clear-cut.

Density Estimation

GMMs estimate the underlying probability density function of data. This is valuable in scenarios where understanding the data distribution is crucial, such as in scientific research or data simulation.

Anomaly Detection

By modelling the normal behaviour of data, GMMs can identify outliers or anomalies that deviate significantly from learned patterns. Applications include fraud detection, network intrusion detection, and error identification in data collection.

Image and Video Processing

In computer vision, GMMs are used for image segmentation (dividing an image into regions based on colour or texture), background subtraction in video surveillance, and object tracking. Each pixel or region is assigned to a Gaussian component, enabling flexible and accurate segmentation.

Speech and Speaker Recognition

GMMs model the statistical properties of speech sounds (phonemes) and are foundational in speech recognition systems. They are also used for speaker identification by capturing unique voice characteristics.

Bioinformatics and Medical Imaging

In bioinformatics, GMMs help cluster gene expression data, detect differentially expressed genes, and identify disease subtypes. In medical imaging, they are used for segmenting tissues, classifying regions, and detecting abnormalities in scans.

Finance and Time Series Analysis

GMMs are applied to model asset price changes, detect volatility regimes, and identify patterns in financial time series. They assist in option pricing, risk management, and predicting market trends,

Recommendation Systems

By modelling user preferences and item attributes, GMMs enhance recommendation engines, enabling more personalized suggestions.

Data Augmentation and Synthetic Data Generation

GMMs can generate synthetic data points that resemble the original dataset, supporting data augmentation for Machine Learning tasks

Closing Thoughts

The Gaussian mixture model is a versatile and powerful tool for clustering and density estimation. Its probabilistic, soft-clustering nature allows it to model complex, overlapping, and non-spherical clusters, making it suitable for a wide range of real-world applications.

While it requires careful selection of the number of components and can be computationally intensive, its flexibility and interpretability make it a staple in the data scientist’s toolkit.

Frequently Asked Questions

What is the Main Advantage of a Gaussian Mixture Model Over K-Means?

A Gaussian mixture model provides soft clustering, assigning probabilities to data points for belonging to each cluster, and can model elliptical clusters, unlike K-Means which uses hard assignments and assumes spherical clusters.

How Do I Determine the Optimal Number of Components in a GMM?

Use model selection criteria like Bayesian Information Criterion (BIC), Akaike Information Criterion (AIC), or cross-validation to balance model fit and complexity, helping avoid overfitting while capturing meaningful clusters.

In Which Scenarios Should I Prefer a Gaussian Mixture Model?

Choose GMM when your data has overlapping clusters, non-spherical shapes, or when you need probabilistic cluster assignments, such as in customer segmentation, image analysis, or anomaly detection tasks.