Bayesian Machine Learning Explained

Summary: Bayesian Machine Learning combines prior knowledge with observed data to update beliefs, providing probabilistic predictions and uncertainty quantification. Ideal for low-data scenarios, it enhances interpretability and robustness but faces computational complexity and prior-selection challenges. Widely used in healthcare, finance, and adaptive systems.

Introduction to Bayesian Machine Learning

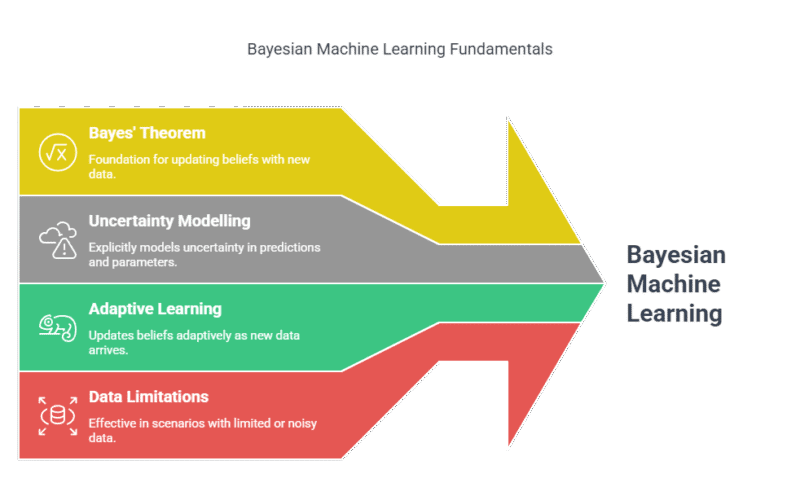
Bayesian Machine Learning is a powerful paradigm that treats model parameters and predictions as probability distributions rather than fixed values. Rooted in Bayes’ theorem, this approach allows for explicit modelling of uncertainty, making it especially valuable in fields where data is limited, noisy, or where quantifying confidence in predictions is crucial.

Unlike traditional (frequentist) methods that provide point estimates, Bayesian methods update beliefs about model parameters as new data arrives, resulting in a flexible, adaptive learning process.

This blog explores the fundamentals, key concepts, methodologies, advantages, and challenges of Bayesian Machine Learning, providing a comprehensive guide for data scientists and enthusiasts.

Key Takeaways:

• Explicit uncertainty quantification enables risk-aware decisions via probability distributions.
• Prior knowledge integration improves accuracy in low-data or expert-driven domains.
• Adaptive learning updates models iteratively as new data becomes available.
• Computational complexity limits scalability for large datasets or complex models.
• Interpretability through posterior distributions aids transparent decision-making.

Understanding Bayes’ Theorem

At the core of Bayesian Machine Learning lies Bayes’ theorem, a foundational principle in probability theory. Bayes’ theorem describes how to update the probability of a hypothesis as more evidence or information becomes available.

Mathematically, Bayes’ theorem is expressed as:

Where:

• P(A∣B)P(A∣B) is the posterior probability: the probability of hypothesis AA given observed evidence BB.
• P(B∣A)P(B∣A) is the likelihood: the probability of observing BB if AA is true.
• P(A)P(A) is the prior probability: the initial belief about AA before observing BB.
• P(B)P(B) is the marginal likelihood or evidence: the total probability of observing BB under all hypotheses

How Bayesian Inference Works in Machine Learning

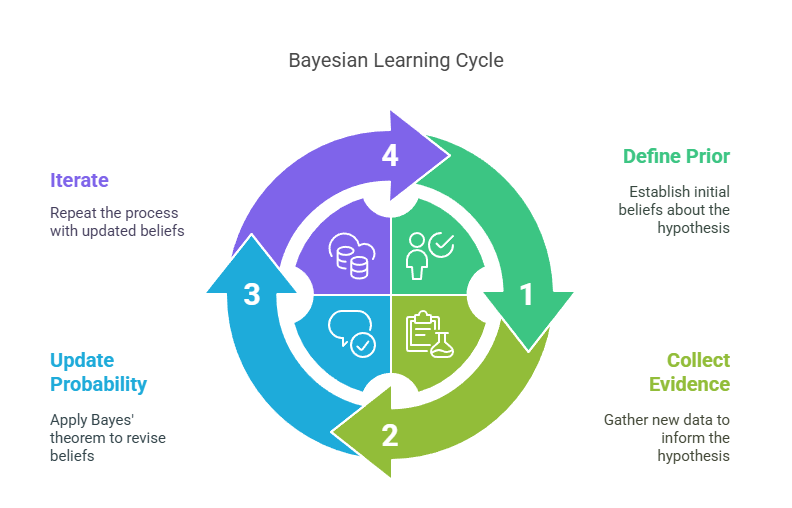
Bayesian inference in Machine Learning is a probabilistic approach that enables models to update their beliefs about parameters or hypotheses as new data becomes available. This process is grounded in Bayes’ theorem, which mathematically combines prior knowledge with observed evidence to form updated, data-driven conclusions.

Step 1: Define a Prior

Start by specifying a prior probability distribution, which encodes your initial beliefs about the model parameters before observing any data. This prior can be based on previous knowledge, expert opinion, or chosen for mathematical convenience.

Step 2: Collect Data and Compute Likelihood

Gather new data and calculate the likelihood, which measures how probable the observed data is under different parameter values. The likelihood function quantifies the fit between the model and the data.

Apply Bayes’ Theorem

Use Bayes’ theorem to combine the prior and the likelihood, resulting in the posterior probability distribution. The formula is:

Where:

• P(θ∣x)P(θ∣x) is the posterior (updated belief about parameters θθ given data xx),
• P(x∣θ)P(x∣θ) is the likelihood,
• P(θ)P(θ) is the prior,
• P(x)P(x) is the marginal likelihood (normalizing constant).

Step 4: Update and Iterate

The posterior distribution now reflects the updated belief after observing the data. If more data becomes available, this posterior can serve as the new prior, and the process repeats—enabling continual learning and adaptation.

Why Use Bayesian Inference in ML?

Bayesian inference enables uncertainty-aware predictions, integrates prior knowledge, and adapts models iteratively. Ideal for low-data scenarios, it enhances robustness and interpretability in risk-sensitive domains like healthcare and finance.

• Uncertainty Quantification: Bayesian inference provides a principled way to quantify uncertainty in model parameters and predictions, which is crucial in real-world decision-making.
• Incorporation of Prior Knowledge: It allows integration of domain expertise or previous findings into the learning process, making models more robust, especially when data is limited.
• Adaptive Learning: As new data arrives, models can be updated efficiently without retraining from scratch, supporting dynamic and evolving environments

Bayesian Methods in Machine Learning

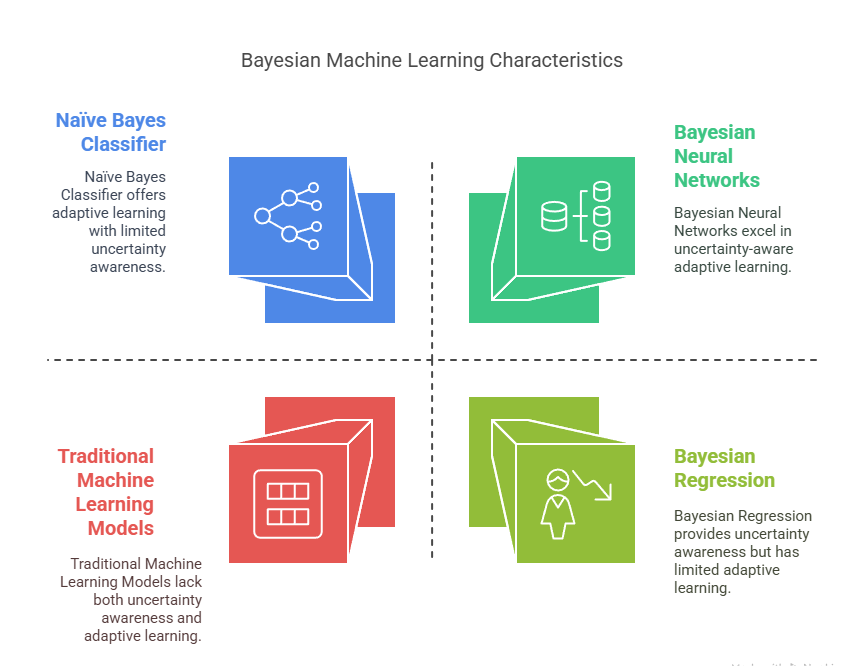
Bayesian methods in Machine Learning combine prior knowledge with data to update probabilistic models, enabling uncertainty-aware predictions and adaptive learning for robust decision-making in dynamic environments.

Naïve Bayes Classifier

The Naïve Bayes classifier is a simple yet powerful probabilistic model based on Bayes’ theorem. It assumes that features are conditionally independent given the class label, which simplifies computation. Despite its simplicity, Naïve Bayes performs remarkably well in text classification, spam detection, and other applications.

How it works:

• Computes the posterior probability for each class given the input features.
• Assigns the class with the highest posterior probability to the input.

P(Class∣Features)∝P(Features∣Class)⋅P(Class)P(Class∣Features)∝P(Features∣Class)⋅P(Class)

Bayesian Neural Networks (BNNs)

Bayesian Neural Networks extend traditional neural networks by placing probability distributions over their weights instead of fixed values. This enables BNNs to model uncertainty in predictions, making them robust to overfitting and better suited for tasks where understanding confidence is important.

Key features:

• Each weight is a distribution, not a single value.
• Training involves inferring the posterior distribution over weights.
• Predictions incorporate uncertainty, yielding not just point estimates but credible intervals.

Markov Chain Monte Carlo (MCMC)

Markov Chain Monte Carlo (MCMC) is a family of algorithms for sampling from complex probability distributions, especially when the posterior cannot be computed analytically. MCMC methods, such as the Metropolis-Hastings and Gibbs sampling algorithms, are widely used in Bayesian Machine Learning to approximate posterior distributions.

How it works:

• Constructs a Markov chain whose stationary distribution is the target posterior.
• Generates samples that can be used to estimate expectations, variances, and other statistics of interest.

Advantages of Bayesian Machine Learning

Bayesian Machine Learning offers significant advantages by allowing models to incorporate prior knowledge, handle uncertainty, and update predictions as new data arrives. This approach improves accuracy, reduces data requirements, and enables flexible, probabilistic decision-making in uncertain environments, making it increasingly valuable for modern Machine Learning applications.

Explicit Uncertainty Quantification

Bayesian methods produce probability distributions over parameters and predictions, enabling robust uncertainty estimates (e.g., credible intervals). This is critical in high-stakes domains like healthcare and finance, where understanding confidence in predictions is essential.

Incorporation of Prior Knowledge

Priors allow integration of domain expertise or historical data, improving model performance in low-data scenarios. For example, bioinformatics tools like Mutect2 use priors to enhance DNA variant calling accuracy.

Adaptive Learning via Bayesian Updating

Models iteratively refine beliefs as new data arrives, making them ideal for online/sequential learning. The posterior from one update becomes the prior for the next, enabling dynamic adaptation.

Robustness in Low-Data Regimes

Bayesian models outperform traditional methods when data is scarce by leveraging priors to compensate for limited observations. This is particularly useful in medical diagnosis or rare-event prediction.

Model Selection and Averaging

Bayesian model comparison uses posterior probabilities to select optimal models, while model averaging combines predictions from multiple models, reducing overfitting and improving generalization

Challenges and Limitations of Bayesian Machine Learning

Bayesian Machine Learning offers powerful tools for uncertainty quantification and the integration of prior knowledge, but its practical application comes with significant challenges and limitations. Understanding these hurdles is crucial for practitioners aiming to implement Bayesian methods effectively.

Computational Complexity

Bayesian inference often requires integrating over high-dimensional probability distributions, which can be computationally intensive and time-consuming. For complex models or large datasets, exact solutions are usually intractable, necessitating approximate methods such as Markov Chain Monte Carlo (MCMC) or variational inference.

These methods can be slow to converge and may require substantial computational resources, posing scalability challenges for real-world applications.

Choice and Specification of Priors

Selecting appropriate prior distributions is a fundamental aspect of Bayesian modelling, but it is also a source of considerable difficulty and debate. Priors can be subjective, and disagreements often arise over how to represent prior knowledge or ignorance.

Poorly chosen priors can bias results or lead to misleading inferences, especially when data is limited. Developing objective or noninformative priors remains an ongoing challenge in the field.

Model Misspecification and Flexibility

Bayesian methods assume that the true data-generating process is represented within the chosen model and prior. If the model is misspecified or important hypotheses are omitted, Bayesian inference can produce unreliable results.

Furthermore, the standard Bayesian framework does not easily accommodate the introduction of new hypotheses or model structures after learning has begun, limiting adaptability in dynamic environments

Conclusion: The Future of Bayesian Machine Learning

Bayesian Machine Learning stands at the forefront of modern data science, offering a principled, flexible, and interpretable framework for modelling uncertainty. As computational tools and probabilistic programming frameworks advance, Bayesian methods are becoming more accessible and scalable.

The future promises deeper integration of Bayesian approaches in real-world applications, from healthcare and finance to autonomous systems and scientific discovery.

Embracing Bayesian Machine Learning equips practitioners with the tools to make more informed, reliable, and transparent decisions in an increasingly data-driven world.

Frequently Asked Questions

What Is the Main Advantage of Bayesian Machine Learning Over Traditional Methods?

Bayesian Machine Learning explicitly models uncertainty by providing probability distributions over predictions and parameters, allowing for more robust, interpretable, and adaptive decision-making, especially in situations with limited or noisy data.

How Does Bayesian Updating Work in Practice? 

Bayesian updating involves applying Bayes’ theorem iteratively: the posterior from one round of data becomes the prior for the next, allowing the model to refine its beliefs as new information is observed.

What Are Common Applications of Bayesian Methods in Machine Learning?

Bayesian methods are widely used in spam filtering, medical diagnosis, recommendation systems, time-series forecasting, and any domain where quantifying uncertainty and incorporating prior knowledge are valuable.